What is a balanced Catan board?

With more than 22 million copies sold since its creation, Catan is, without doubt, one of the most played board games in the world.

There are many reasons for the game success: its gameplay is simple, fast, and offers a good balance between luck and strategy.

But with time, and the recent explosive diversification of board games, it is not hard to find Catan detractors! But there is a ton of enthusiast Catan players, and even if I often tend to gravitate towards heavier games, I count myself among them!

Criticisms of games are often interesting because there is often some truth to them. So I decided to investigate some and see what we can learn from them.

(But I just want some fair or unfair Catan boards to play)

Jump right here to see examples of Balanced Catan boards.

Or if your prefer: Unbalanced Catan boards.

If however, you are interested in how I came up with those, read on, I think this is the interesting part!

Ok, here we go ->

Recurrent Catan criticisms

If you are familiar with online board game communities, you’ll often read criticism of Catan among the following lines:

• The game relies too much on randomness, with too many dice rolls.
• The initial setup of the island is often unbalanced, making some resources hard to get.
• The game is unfair, starting position usually determining who will win from the start.

It is easy to spot an apparent contradiction:

The winner is determined by the luck of dice during the game

OR

The winner is mostly determined by starting position (and mostly unaffected by what follows.)

You see, we already have a good mystery on our hands!

What to expect in this article

In today’s post, we will address the initial setup of the game, and try to answer the following question:

What is a balanced Catan board?

And to get started on this, we will do 4 things:

• Quickly look at what is the Catan Island initial setup
• Establish the difference between a balanced setup and a fair setup.
• Find an objective way to measure if a Catan island is well-balanced.
• Have a look at different initial boards and even have a peek at extreme board setups!

Here is a preview of my new metric, the Catan Island Balance Index:

Going deeper

Once you start digging into board balance, a more complex question quickly emerges:

Is a balanced board inherently fair?

In my next article, I’ll have a deeper look at how the players choose their first settlement and try to determine if the first, or last player has the most to gain by playing on certain boards! We will then try to determine what is a fair or unfair board and if balanced boards are fairer than others! (The fair Catan board quest)

(Here is a sneak peek of a settlement selection simulation, when ignoring the resource types)

The randomness question should be addressed in a later article, where I’ll try to give some hard evidence that luck does not play that big of a role in the game. But since it is mainly an intuition at the moment, maybe the numbers will surprise us!

But balance and fairness is already a big program, so let’s start with that. Hopefully, we will gain some insights about Catan and maybe become better players in the process!

If you wish to skip the initial setup explanation: Start here

Laying out the game context

A Catan game is played on an imaginary island, composed of:

• 19 hexagonal resources tiles.
• 18 of them associated with a number from 2 to 12.
• 9 Harbors allowing a better rate of exchange for resources.

The hexagon tiles

Hexagonal resource tiles are placed one in the middle, and the rest making two concentric circles around it.

There are 6 different types of tiles (each producing a different resource):

• 4 Fields (Grain)
• 4 Pastures (Wool)
• 4 Forest (Lumber)
• 3 Hills (Bricks)
• 3 Mountains (Ore)
• 1 Desert Tile ( No production )

The Numbers

Each tile on the island is attributed a number (except the desert tile).

The numbers go from 2 to 12, each being present twice except 2 and 12.

During the game, at the beginning of each player’s turn, the player rolls a pair of dice. The sum of both indicates which resources tiles will pay out. Each settlement around those tiles will produce one resource card for its owner (2 resource cards if the settlement was upgraded to a city).

The only restriction on how the numbers are placed is that high probabilities number, like 6 or 8, cannot be on adjacent tiles.

Harbors

Harbors are placed around the island as if they were on their own sea hexagon. Each connects with two hexagon corners, and are placed with at most one harbor connection per settlement positions around the island.

During her turn, a player can exchange 4 resource cards of the same type against 1 resource card of her choice.

The harbors allow players to trade resource cards at a better exchange rate than the default.

Five harbors are of a specific resource type (one for each resource type). They allow an exchange rate of 2 cards of the harbor type against 1 card of any type (Noted 2:1 on the map).

Four harbors are neutral harbors allowing exchanging 3 cards of one type against 1 card of any type (Noted by 3:1 on the map).

Initial settlement placement

The first step in the game is to place initial settlements on the board.

Settlements are placed at the corners of hexagons. And thus are associated with between 1 and 3 hexagons, depending on where they are placed. Roads are placed on the side of hexagons and are used to connect settlements.

Settlements cannot be placed next to each other. They need at least one empty settlement position between them.

In the beginning, each player place, in-turn, one settlement, and one attached road. When this is done, they all place a second settlement-road combo, but in reverse order.

So the player order is: 1-2-3-4 4-3-2-1

To complicate things, each player receives one resource card for each tile surrounding its second settlement. Thus making it a tough choice of securing a good location, or deciding to get an early advantage by starting with known resource cards, but a lower resource payout.

It is important to note:

• Resources are not of equal importance during the game,
• Some resources are scarcer than others on the island.
• Tile associated numbers don’t have the same probabilities of coming up.

All of this makes certain spots on the island much more interesting than others…

Are some initial board setups unfair?

First, two important definitions:

A balanced Catan board is a board where resources and roll probabilities are equally distributed on the board, but also where probabilities are well distributed among resources types.

A fair Catan board is a board where all players have an equal chance of selecting good starting positions, no matter in which order they play.

Fairness and balance are not necessarily the same thing. And since balance is easier to determine than fairness, let’s start with balance. It will come up handy when attacking the fairness question…

How to decide on the initial Catan board setup

When setting the game up, you have basically two choices:

• Playing on the suggested beginner board setup.
• Randomizing the tiles to play on a unique setup.

The first option can only last so long since it gets tiresome to always play the same initial board.

Randomizing the board is an easy way to offer game variation without having to buy a game extension. And frankly, you gain a lot of understanding of the game by trying to find what makes for a good starting position on an always renewed game setup.

You can read my take on the importance of offering game variation 
in my previous post: Flamme Rouge a Study of Game Variability

However, it is inevitable that sometimes people will find that a random board can be unbalanced, making it hard for them to place their initial settlements on positions offering them a good assortment of resources, with reasonable dice probability associated with them.

Can we come up with a good metric to objectively measure if a board is well-balanced? This would certainly be helpful to agree on an acceptable initial setup for all!

Establishing an objective measure of Balance

Let’s start with the following assumption:

If resources and probabilities are well distributed on the board, there will be numerous equivalent starting positions. Players should then have similar chances to win at the beginning of a game.

Since measuring the element distribution is a pretty simple idea, I decided to come up with an objective way to measure how balanced is a Catan Board in terms of its initial setup.

I even gave it a name: The Catan Island Balanced index or CIBI.

Little known fact:

Cibi is also the name of a Fijian war dance.

In 1939, when Fiji prepared for its first-ever tour of New Zealand, the captain, Ratu Sir George Cakobau, thought his team should have a war dance to match the All Blacks’ haka. He approached Ratu Bola, the high chief of the warrior clan of Navusaradave in Bau,who taught them the Cibi which has been adopted as Fiji’s pre-match ritual ever since and went on to become the only team to remain unbeaten on a full tour of New Zealand.

Extract from WIkipedia.

And since Catan is a competitive game taking place on an island, it is a rather fitting name!

So let’s describe what is in effect the CIBI index 1.0.

I may revisit this later if people show interest in the idea, or if I or others discover better ways to approach it, but I think it is a very good conversation starter on the subject!

What makes a Catan board well balanced

As I explained earlier, there are three elements that combine to form a Catan Island:

• Resource Tiles (What resource are produced)
• Roll Numbers (When resource are produced)
• Harbors (Allowing favorable exchange rates for resources)

How those three elements are combined is what makes a board well-balanced or not. I chose 6 different measures of balance and combined them for the ultimate balance index:

• Resources distribution on the island
• Resources clustering
• Probability distribution on the island
• Number Clustering
• Probability distribution per resources
• Harbor placement by resource type

Here is an explanation for each of those:

Measuring distribution

In order to measure if resources or probabilities are evenly distributed across the Catan island, I decided to measure how well things are spread on the board by dividing the island into equal parts.

There are different ways of splitting the island in two. I decided to do it in a way that would separate the locations of the settlements into two groups, without any sitting on the dividing line.

As shown in the following diagram, there is three easy way to do so:

Here how it is used for the resource distribution:

Resources distribution on the island

Because the spatial distribution of resources is the first thing people see when looking at a Catan board, resource distribution felt like a good element to include in a balance measure.

How to calculate it:

First, consider each possible settlement position and count the frequency of connected resources for each. Those numbers are used to calculate the distribution of resources in the following manner:

Considering one dividing line at the time:

• For each side, sum the frequency of each available resource.
• Compute the difference between sides for each resource type.
• Sum the square of each difference for the final score

Doing this for each 3 dividing line and summing it up gives us our Resource distribution score.

To illustrate, here is the contribution to the score by the forest resource tiles, for one of the three separation lines (36).

By doing this for each resource and each separation line we get a number that represents the resource distribution balance. The lower the more balanced, the higher, the less balanced.

If you wonder why I squared the number, it is simply to give more weight to a large imbalance for one resource than for several small imbalances over several resources!

Here how it looks on selected randomly-generated boards, shown here from most balanced to less balanced:

While I bring everything back to a scale from 0.0 to 1.0* later on, I thought showing the raw numbers could be interesting.

Note that the lowest score found for a board is 0, meaning that the island if perfectly balanced in terms of resources when it comes to the 3 dividing lines. This measure cannot go lower, so it shows the limit of this metric.

The upper limit is, however, a soft limit. I did not explicitly calculate the theoretical upper limit, nor I am claiming this is the most unbalance a board can be.

The way I proceeded was to generate 100 million random boards, score them, and keep the highest and lowest scoring boards. (Actually, I did this a couple of times and updated the highest scores if I found one, but this is essentially the same thing). I think it is a fair approach, let me know if you disagree!

While the resource distribution on the island component gives an interesting measure, it is not the only component of resource distribution. Even with a score of 0, we can see some resource clustering.

So I decided to add a measure to specifically address that issue.

Resource clustering

In order to verify that resources are not all clustered in one group on the board, I added a simple clustering measure:

Each time two hexagons of the same type shared an edge, I counted 5 points.

That’s it!

Here are five islands from less clustered to most clustered with their respective score:

Note here than in the most balanced board, there are no tiles of the same type sharing a border!

Because the resource clustering could be seen a bit redundant with the previous resource distribution measure, I decided to have a look at how correlated those two are. Just so see if both measure the same thing.

To do that, I simply created a graph relating both measures for every board. Each dot on the following graph is a different island:

We can see that both measures are correlated, but they are definitively not the same! You can still have some clustering in a perfectly mirrored island, and not all imbalanced mirror images are fully clustered.

(For the math geek, they have a Pearson correlation coefficient of: 0.686)

A future CIBI index could maybe do with only one of the above, but I felt inclined to keeping both for the moment!

Probability distribution per resources

On a randomly generated board, it would be surprising that each resource ends up with the same probability of producing on the island.

To consider the fairness of the probability distribution per resource type, I started with the following assumption:

• Resources should have a total probability of paying out proportional to their presence on the board.

So for each resource type, I considered the expected return (resource production) of all the tiles over 36 dice rolls. This is easy to do since this is represented by the number of dots under each number.

For example, a resource hexagon associated with the number 5, should be expected to pay out 4 times every 36 dice rolls (on average).

There is a total of 58 dots for all the numbers in play. The most frequent result of a dice roll is 7, with an expected count of 6… But there is no number 7 on a Catan board, this number being instead used to activate the robber.

There are 30 dots under the remaining numbers from 2 to 12. And each number is on the board twice, except 2 and 12. So for the duplicate numbers we have also 30 dots, minus the 2 dots that would have been under the 2 and the 12. So we have 30 + (30 -2) = 58 dots on the island

58 dots distributed over 18 hexagon tiles.

Resources that have 4 associated tiles should get on average:

4 * 58 / 18 = 12.889 expected payout (Grain, Wool, Lumber)

And similarly, resources with 3 associated tiles should get on average:

3 * 58 / 18 = 9.667 expected payout (Brick, Ore)

How to calculate our measure of resource probability distribution:

• Add up the associated roll number probabilities over 36 rolls for each resource type (Count the dots under the numbers for each resource).
• Square the difference between expected and actual probabilities for each resource type.
• Sum all the square differences!

Here is a progression from balanced to completely unbalanced probabilities distribution for the resources:

It is interesting to note that here the lowest score is 1.0 instead of 0. It is simply because since we consider the expected payout, the numbers are not round numbers, and so as balanced you try to be, you are always left with resources being slightly over or slightly under than the unattainable number, just a quirk of the choice of measure that we have to live with!

Probability distribution on the board

The thinking for the probability distribution is similar to the one for the resource distribution, except that instead of counting the number of resources tiles, we count the probabilities of getting resources for each settlement for both sides of the mirror lines.

The point is to make sure that the probabilities of getting resources are well balanced between each part of the island.

As for the resources distribution, I did the following for each of the three possible ways of dividing the island:

• For each settlement position, count the number of dots under the numbers on each surrounding tile.
• Sum the settlements scores for each half of the island.
• Square the score difference between both halves.

Adding the final score for each dividing line gives us the final score.

Here are five islands from most distributed to least equally distributed:

Number clustering

One of the most treacherous things in Catan is settlements touching two different tiles with the same number. Especially if this number is not coming up as often as the statistics would have us believe it should.

If the actual numbers are regrouped on the board, it has the potential to augments greatly the unfairness of unlucky dice rolling, and thus should be considered a factor of unbalance.

Here we are doing a similar thing than for the resources clustering: Adding a score of 5 each time two hexagons with the same number shared an edge.

Here the limit ends up being 30. There are two number tokens for numbers between 3 and 11 inclusively, excluding 7. However, by the rules, we do not consider boards as valid when the two 6s or the two 8s are adjacent.

This leaves us with only 3-4-5-9-10-11 that can be on adjacent tiles. Six numbers potentially scoring 5 each is 30.

(Just a quick note: The number under this one are a bit misleading, due to the way I built those sequences. I picked the best and worse island, determined equally spaced number, and found the board with the closest score to that. So here 7.5 is between 5 and 10, but is actually showing an island with a score of 5).

Here how it looks, from most balanced to the least balanced:

Following the same line of thinking than for the resource distribution and resource clustering, one could think that a number clustering measure would yield similar results than those of the probability distribution measure. But graphing those two together gives a drastically different look!

This time we can see that probability distribution is not at all correlated with number clustering!

If you stop to think about it, this is however not that surprising.

There is a greater variety of numbers than resource types, so comparatively, fewer chances for numbers to be actual neighbors. And since different numbers can have the same probability, it is easier to distribute probabilities around the island without clustering the number at the same time!

(For the sake of completeness, the Pearson Correlation coefficient here is: 0.068)

Harbor placement per resource type

Harbors are an important element of a Catan game. They offer a better exchange rate for resources, allowing you to rely less on the willingness of other players to trade during the game. As such, they can really be part of a winning strategy!

Harbors come in two types:

• 3:1 harbors let you exchange 3 cards of a type against any resource card of your choice.
• 2:1 harbors let you exchange 2 cards of the harbor resource type against the card of your choice.

This makes harbors of a specific type more appealing… if in addition they are connected to a high paying hexagon tile of the same type!

To create a harbor balance measure I decided to give a score to each harbor based on its expected return:

• Count the expected payout of each settlement connected to a harbor (counting as before the dots on the number tiles).
• Payout of the same type than the harbor type count double.
• Harbor’s score is the highest score of the settlements that connect to it.
• Using those, simply calculate the variance.

Here is an example of Harbor Scoring:

For the variance:

• Calculate the return each harbors on the board.
• Calculate the average.
• Then, calculate the square difference between each score and the average.
• Calculate the average of the squared difference

This gives you the variance: the average distance to the average (squared).

For our measure, I kept the sum of squared distance, instead of taking the average, closer in magnitude to the other measures. You can divide by 9 to get the variance if you prefer!

Using this, if all harbors offer a high payout, the measure will be low, meaning we have a balanced board, and if all harbors offer a poor payout, this will also be considered balanced. Only if the values are spread unequally from harbor to harbor will we get a high score!

Here is a sample, from most to least balanced.

To add a bit on this measure: high index values here indicate wildly imbalanced harbor returns, some harbor being really interesting to settle, and others not at all.

The downside is that a lot of balanced harbor situations end up with having mostly barely interesting harbor payouts. Maybe this measure could be improved, but it gives us some interesting thoughts about harbor placement!

How does it all add up

Now that we have all the components of our balance index, how to we put them together?

First, I decided to give equal importance to all previous measures. To do that I reduced each one on a scale from 0.0 to 1.0*.

Note: The 1.0* being the highest value obtained on a 100 million board run, it means that some measure could exceed 1.0 on occasion, but probably not by much!

To combine the 6 measures, I opted for a simple average, this translates in the following:

• Low values should mean that a board scored low on all measures.
• High values should mean that a board scored high on all measures

And Medium values… well… they indicate medium values for all or a mix of high and low values.

There is probably a better way to combine all these metrics, but they often have their own drawbacks. I think the average is a good start. Let me know if you think another method would be more appropriate!

So how does it look like?

To give you an idea, I did the same than for individual measures and extracted boards with representative values from low to high:

As with all synthetic index, the CIBI index gives an idea of the board balance, but looking at it while also including all individual components is much more interesting. So let’s have a look at individual islands with all their associated scores!

Evaluating individual Island

Now that we have an objective measure, we can check how different Island scores on it. And what better place to start than looking at the suggested island for the beginner in the Catan Rule book (at least the one I have here) and see how it fares:

As you can see the beginner island is not perfectly balanced:

• Two pastures hexagon share a tile.
• Hills and mountains have a higher probability per tile.
• The forest harbor is more advantageous than other harbors

For comparison here is the best CIBI index island, out of 100 million generated boards.

It is not perfect either, but it is more balanced than the starter island!

And if we have a look at the worse CIBI balanced board found in 100 million generated islands, we can see it looks a bit nightmarish to play!

Here we can see that the board is quite unbalanced, with heavy clustering of resources and numbers. But surprisingly, it is easy to see that it is not the worse board we could get! Simply shifting the harbors around should give us a higher score on the Harbor Return Balance, and push the CIBI index even higher!

This shows that the number of possible Catan board is extremely high!

Even after looking at 100 million random boards, we can easily see how we can make the worse of the random board even worse. It means that those 100 million are only a tiny fraction of all possible island arrangements. There are extreme boards to be found in this large space for sure!

Looking at boards from the 100 million generated boards

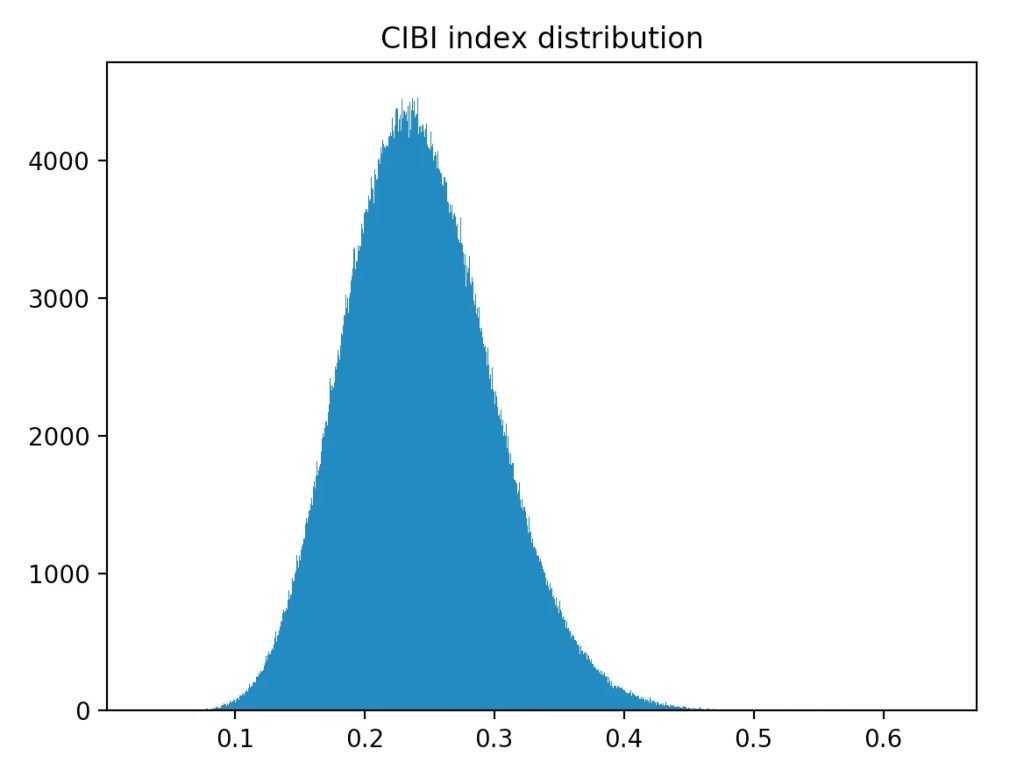
Over a range of 100 million generated random islands, the average CIBI score was 0.243, with a standard deviation of 0.056.

For the curious, here is the CIBI score distribution for the generated boards:

Looking at average boards

Let’s have a look two boards with the average score:

This board has a few elements that score higher, namely the resource clustering, and the number clustering.

The effects of resource clustering are much more eye-catching than those of the number clustering. And the number clustering is a bit fast to get to high-values given that only 2 sets of numbers touching are needed to be at 0.333.

Maybe the resource clustering could be given greater weight in the final index. But no one said that the average should be considered a balance board!

This could merely indicate someone may want to look at lower scoring boards when looking for a truly balanced board!

Here is a second average scoring board

Here the score is again higher on number clustering, with the 9-10-11 in pair. And the Resource probability distribution being less fair.

Here is the breakdown:

• Bricks 7
• Grain 14
• Wool 8
• Ore 12
• Lumber 17

Which looks quite unbalanced, with the Forest having twice the probabilities than the pastures for the same number of tiles!

Is the average scoring board balanced?

On average, placing the elements randomly will make for boards that are playable, but we cannot really say that those are really well-balanced boards.

Building a truly balanced board takes time and needs careful consideration of several factors! (Or, with an objective measure, it only needs for us to define the desired values for each measure, and randomly generate boards until we get one that satisfies those!)

After all this, I think the CIBI measure and its components are a good tool to evaluate a board, allowing to immediately spot balancing issues that would take more time to evaluate by hand!

Comparing to real-life boards

For comparison, let’s check a board that was used in a tournament. (I picked up the first one I found)

Here we can see that this tournament board is pretty well-balanced!

In fact, it would score in the top 0.2% of the 100 million randomly generated board according to our index.

However, we still have some resource clustering, and some parts of the island are being favored in terms of probabilities. So there may be a place for improvement still!

Let’s find some extreme boards!

Note that once we have a highly balanced or unbalanced setup and an easy to compute measure, it is easy to tweak a particular board to get even more extreme setups!

One could:

• Start with the most unbalanced of 100 million only looking at the resources distribution and clustering
• Randomize only numbers on that island to maximize probabilities imbalance and number clustering
• Finally, randomize harbors to get the worst possible board.

How bad can it get? See for yourself!

For this final and truly unbalance board, I think, we managed to find a good 24% higher score. The clusters of everything are obvious, and the probabilities are duly unbalanced for resources and harbors!

I’m actually curious to know how it would play, I’m certainly down for trying it at some point!

To Conclude

I think that overall, the CIBI index is an interesting measure, and at least a good experiment to have. While it can be improved, it is easy to see how it allows for a good evaluation and discussion of what is a balanced board.

And while I do not personally mind unbalanced board, since they make for an interesting puzzle, I think that the CIBI index can be fun, even just to find even more weird puzzle to solve!

Now, I know, the best way for you to get an idea would be to offer a small interactive app, allowing you to build your own island, or randomly generate them and see their score for yourself. But this is a full project in itself. I’ll have a look at it, and see what I can do if enough people show interest in it!

In the meantime, for those who would like to see more fair boards, here are a few you can use until I manage to build a web-based tool for you to play with!

Balanced Catan Board to play with

Unbalanced Catan boards to play

If you are more into chaotic games, here are a bunch of Highly imbalanced boards:

What is next?

Now that we can objectively measure how well balanced is a Catan board, it is time to turn to what I think is the core question:

Are balanced islands fairer?

And by that I mean, if you are the first or the last player to place its settlement at the beginning of the game, do some boards offer an unfair advantage?

If this question interests you, or if you think you know the answer, the next article should be of interest!

Read it here: What is a fair Catan island?

Hope you enjoyed my balance measure analysis!

If you have any comments or suggestions, you are welcome to write in the comments below, it is always a pleasure reading you!